Tips: Excelでの数値表現と計算精度

※ 本項は上級者向けの資料。初心者は読むと混乱する可能性が高いのでオススメしない

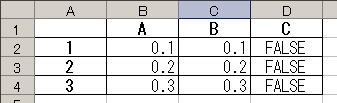
練習問題　「A列に入っているデータはB列に入っているデータと等しい」という計算式をC列に入れなさい

A B C
1 =4.8-4.7 0.1
2 =365.2-365 0.2
3 =135.5-135.2 0.3

単純に考えれば、セル A1は4.8-4.7= 0.1, セル B1 も 0.1 であるから、セル C1 に =A1=B1 という計算式を入れれば結果は TRUEである。以下同様で、セル C2 もセル C3 も TRUEとなるのが「アッタリマエ」である。しかし、実際にこの計算を行ってみると以下のように全て FALSEとなる。なぜ？

1. 無限小数を含む計算を有限桁数で計算すると何が起きるか

たとえば、1÷3を計算して、その答えに3を乗ずる計算を考えてみよう。1÷3は 0.333333333…であるから、紙に中間の結果を書こうとするといつまでたっても終わらない。それでは困るので、中間の計算結果では小数点以下10桁まで書くというルールを（便宜的に）作る。すると、

1÷3 = 0.3333333333
0.3333333333×3=0.999999999

あれ。1÷3に3を乗じたのに、1に戻っていない。この場合、誤差は0.00000000009999999999999…となる。計算目的によって、この程度の誤差が問題になるか否かは異なるが、「有限桁数で計算すると誤差がでることがある」ということは直観的に理解できる。Excelでの（Excelに限らず、コンピューター一般に言えることだが）計算は、無限の桁数を扱えるわけがないのでどうしてもこの制約がある。

1.1 2進数で考えると、10進数の0.1は無限小数

でも、上に出てきた例は切りがいい0.1になる計算だった。なぜうまくいかないのだろう？　それは、Excelの内部処理が人間になじみのある10進数ではなく2進数で行われているから。10進数の0.1は、2進数で表記すると

0.1 × 2 = 0.2 → 0
0.2 × 2 = 0.4 → 0
0.4 × 2 = 0.8 → 0
0.8 × 2 = 1.6 → 1
0.6 × 2 = 1.2 → 1
0.2 × 2 = 0.4 → 0
0.4 × 2 = 0.8 → 0
0.8 × 2 = 1.6 → 1
0.6 × 2 = 1.2 → 1
0.2 × 2 = 0.4 → 0
……
という計算から、0.0001100110…と無限小数になる。無限小数を有限桁数で記憶するわけであるから、2進数で計算している Excelでは、実は 0.1 を正しく記述することはできないことになる。実際に、どの程度の桁数まで扱えるかを調べる方法として1に小さい数εを足して、1+ε>1となる範囲を探すという方法がある。このような条件を満たす最小のεをマシン　イプシロン（machine epsilon）と呼ぶ。

1.2 Excelのマシンε

Excelの内部処理が2進ということはわかっているので、2のべき乗の値でεを探索した結果が下の表である。

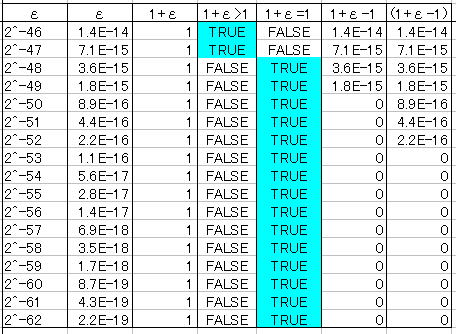
どうもExcelはとても奇々怪々な内部処理を行っているらしい。パソコンなどでよく使われる数表現では、マシンεは2-52になっていることが多い。でもExcelでは 1との差が0になるかどうかは計算式全体を（）で括った場合と括らなかった場合で異なる。もちろん数学的にカッコがついていてもついていなくても同じなのだが、Excelは違う処理をするようだ。カッコなし（普通の計算）だと、2-49あたりがεのようなのだが、カッコをつけると内部的には2-52まで計算に使っているようである。このへんの3桁について、Excelがどうやって処理しているのかはちょっと調べた限りではよくわからなかったが、Excelで 1/3に3を乗ずると1になる謎はこのへんでこっそり Excelが誤差を隠しているような感じ。

1.3 数値の比較

冒頭の例で挙げたケースは、もともと誤差があることをユーザーから一生懸命隠していた Excelの努力が破綻した瞬間と言っていいだろう。A列とB列の差をとると、10-16くらいのオーダーでも等しくないとなっていたりして、上の表の結果とも少し違う。比較対象が1なのと、0.1で誤差として認める範囲を変えたりしているのだろうか。0.1+ε=0.1となる条件でチェックすると、今度は10-16のオーダーで判定しているようなので、やはり比較対象との相対的な誤差が10-15くらいのところで大小関係の基準は決まっているような感じである。ただし、正式なドキュメントを発見できたわけではないので詳細は不明。

2. では、どうすればいいのか

Excelに限らず、実数を有限の桁数で表したり計算したりすれば必ず誤差がでるし、計算回数が増えれば誤差はどんどん蓄積していく。実は計算順序によって結果が違うこともあるので、Excelの再計算のようにどういう順番で計算してるんだかよく分からないものが絡むとますます話がややこしくなる。まず意識すべきことは、コンピューターは有限桁数で計算するので、計算誤差は必ずある

2.1. 必要な桁数だけ使って、要らない部分は捨てる

大体のケースでは、Excelの見た目の計算精度は15桁程度あるので、必要な数字の有効桁数があまり多くなければ下の方の桁は誤差だと思って結果を使わなければ大きな問題はでない。

A B C
=4.8-4.7 0.1 =ROUND(A1,1)=ROUND(B1)

単純な計算については最終的なデータを出す段階で有効桁数を考えれば問題がないことも多い。ただし、最初から桁数の多い数値を扱うときは注意が必要。たとえば日本の公債発行残高を1円単位で扱いたいとなると、Excelでは相当厳しい。1000兆円と1000兆+1円はExcelでは同じ額として扱われてしまう。

なお、この場合では要らない部分を捨てるために四捨五入処理が必要になるが、四捨五入の際には数値の比較を内部的に行う。2.3の数値比較に関する注意は必要な桁数だけ使う場合にも有効である。

2.2. データを最初から整数になるように桁をずらして処理する

加減乗算しか出てこないような集計であれば、あらかじめデータを適当なだけ桁をずらして整数にして処理すれば小数を有限桁で打ち切ることによる誤差はでない。最初の例にあった4.8-4.7と 0.1の比較であれば、全部10倍しておいて

A B C
1 =48-47 1 =A1=B1

のように処理すれば、小数を2進数に変換する際の誤差は防げる。しかし、有限桁で扱っている以上、除算が入ればどちらにしろ誤差が出てくることは避けにくいし、数値自体が大きくなった場合はやはり誤差が出てくる。

2.3 比較は誤差の影響を考えて行う

実際にExcel内部で何をやっているのか分からないが、Excelが比較で使う誤差範囲は相対誤差で10-15のオーダーのようである。これは、見た目の計算精度が15桁ということと整合的にしてあるのだろう。実際には上の例で挙げたように1回の計算でもこれ以上の誤差がでることがある。この場合は、明示的に許容できる誤差範囲を指定することで比較を正しく行うことができる。

1 相対誤差と絶対誤差

ある値 a に対して、コンピュータ処理した結果得られたものが 誤差 Eを含んだ値 xであるとしよう。このとき、

絶対誤差 EA=| x - a |
相対誤差 ER=( x - a ) / a

と定義する。絶対誤差は、扱っている数値の大小によって適切に大きさを変える必要があるが、相対誤差はその手間はない。ただし、除算が入るため余計な計算時間がかかるのと、aが 0に近い時は別扱いを考える必要があったりするのが若干面倒。どちらも一長一短である。

2 誤差を考えた「等しい」の判定

以下では、絶対誤差と相対誤差を特に使い分けず、誤差として扱っても構わない程度の小さい数（*1）εを考えて説明する。このとき、真の値 a　対してコンピュータ処理した結果得られた数値 xが

a - ε < x < a + ε

の範囲に入っていれば、a と xは「まぁ等しい」と考えることにすれば、xにいろいろな誤差が入っていてもεより十分小さければあまり問題はない。

たとえば、一番最初の練習問題で 4.8 - 4.7 を 0.1と比較しているが、

「元の数字は 4.8 と 4.7 なので、有効桁数は高々 2桁、小数点以下はそもそもあまり信用できない数」

ということを前提にすれば、このケースではεとして 0.01くらいを使えば結果が 0.1と等しいかどうか言ってもいいだろう。これをExcelの計算式で書くと、セル C1 に =ABS(A1-0.1)<0.01 と入力することになる(*2)。ABS関数は、引数の絶対値を返す関数なので、A1と0.1の差の絶対値が 0.01未満であれば「まぁ等しい」とみなしている。A=Bという条件は、A-B=0と書き換えられることを利用しているわけだ。もちろん、この 0.01という数は実際に計算する人が「これくらいなら許容できる」ということできちんと決める必要がある。

（*1）εをどの程度の大きさに設定するかは、そのとき扱っている数値の有効桁数や求められる結果の精度に依存する。これをどう決めるかは知性とバランス感覚が要求されるため、最初から相対精度で10-15くらいと決めてしまう Excelのやり方にはかなり問題がある。

（*2）もっと素直にAND(0.1-0.01<A1,A1<0.1+0.01) と書いても全く構わない。ABS関数なんかでコンパクトに書きたがるのは、1文字でもタイプを少なくしたい、少しでも処理を速くしたいというコンピューター屋のケチ根性がしみ出している。

3. 誤差を考えた大小の判定

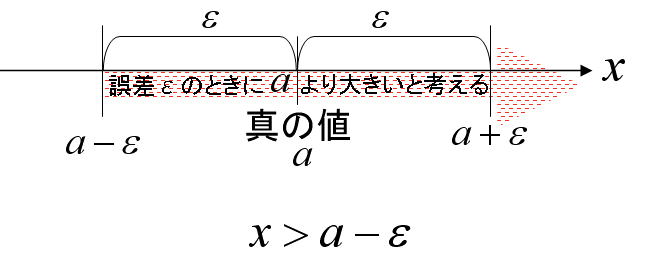
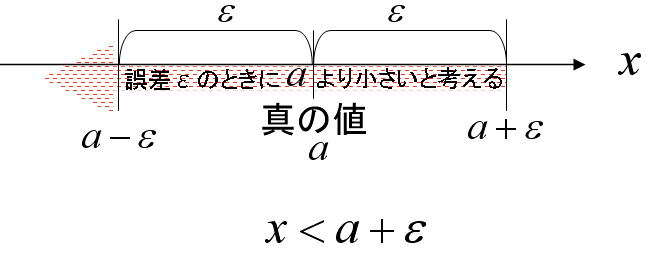
次は誤差εを含んだコンピューター内部の数 x と真の値 a の大小比較を考えてみよう。大小比較であっても、考え方は等しい場合と全く同じである。この場合は、真の値 a　対してコンピュータ処理した結果得られた数値 xが

a - ε < x

であれば、x > a と判断できる。また

x < a + ε

の範囲に入っていれば、a > x と判断してもεが十分小さければあまり問題はない。これらの関係を図示すると、以下のようになる。

たとえば、セル A1 の値が 0.1 より大きいという論理式は、εが 0.01の場合

=A1-0.01>0.1

と書くことができる（*3）。また、同様にセル B1 の値が 1.414 より小さいという論理式は、εが 0.0001ならば

=B1+0.0001 < 1.414

と書くことができる。

4. 四捨五入と誤差

四捨五入操作も、Excelの内部表現の制限を逃れることはできない。そのため、適切なサイズのεを使って比較が正しく行われるよう補正する方がよい。