2007年度経済情報処理
| A | B | C | |
|---|---|---|---|
| 1 | 会社名 | 売上高 | 市場占有率 |
| 2 | きつね食品 | 192 | ? |
| 3 | たぬき物産 | 168 | ? |
| 4 | いなり商事 | 224 | ? |
| 5 | 合計 | ? | ? |
例題1. 消費税の計算で1円未満の端数が出た場合の切り捨て処理を行う
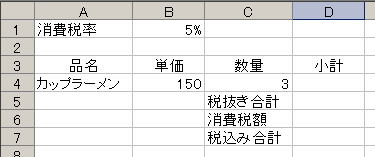
消費税が5%のとき、150円のカップラーメンを3個購入した。消費税額と、消費税込みの支払い総額は幾らになるかを求めてみよう。(*3)
Step 1. データを入力する
まず、計算に必要な基礎データと説明用の文字列を入力する。Excelは単に 5% と入力すると、自動的に0.05と解釈してくれるので便利。

Step 2. 計算式をとりあえず入力する
ここまで学んだ計算式の作り方を思い出して、
を入力すればよい。計算式が入ると、こんな感じになる。しかし、このままだと消費税額に1円未満の端数がついてしまうので、切り捨て処理を行いたい。
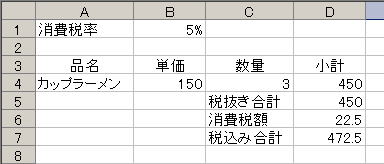
Step 3. 切り捨て処理を INT 関数で行う
切り捨て処理のような操作は、ここまでに出てきた四則演算の範囲ではできない(*4)。Excelでは、このような処理を行うためにいくつかの関数があるが、ここでは一番単純な INT 関数を用いる。INT関数は、数値を一つ与えると、戻り値としては引数を超えない最大の整数を戻す関数である。INT関数に与えられるものは、
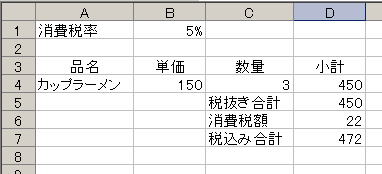
のいずれでもよい。もちろん、参照先のセルに入っている値や計算式の結果が数値でなければエラーとなる。この例題では、セル D6 の消費税額の1円未満を切り捨てたいので、セル D6 を以下のように書き換える
すると、小数点以下が切り捨てられて下のような計算結果となる。
(*3)現在は税込価格での表示が原則であり、税込価格に含まれる消費税相当額は「税込価格×5/105」と考えるのが原則。税抜価格から消費税額を求めて表示するという扱いは適切な操作ではない。詳細は国税庁web(http://www.nta.go.jp/)などを確認のこと。
(*4)セルの表示形式の設定や![]() (小数点表示桁下げボタン)を使って小数点以下を表示しないようにすると、表示上は小数点以下が消えてスッキリするが、データとして小数点以下の値がなくなるわけではないので注意。たとえば、0.3, 0.3, 0.4が入っているセルの表示桁数を変更して、表示上は全部0にしたとしても、この3つのセルの合計を計算するとちゃんと1になる。INT関数で処理した場合とは全く異なる。
(小数点表示桁下げボタン)を使って小数点以下を表示しないようにすると、表示上は小数点以下が消えてスッキリするが、データとして小数点以下の値がなくなるわけではないので注意。たとえば、0.3, 0.3, 0.4が入っているセルの表示桁数を変更して、表示上は全部0にしたとしても、この3つのセルの合計を計算するとちゃんと1になる。INT関数で処理した場合とは全く異なる。
練習問題1. INT関数に以下の数値を与えたとき、関数の戻り値はいくつになるか。まず自分で予想してから、実際に Excelを使って実験してみなさい。
例題2. 関数名が分かっている場合にヘルプを調べる
ヘルプの読み方練習として、まず関数名が分かっている場合を試す。メニューにある「ヘルプ(H)」から「Microsoft Excelのヘルプ(H)」を選び、検索文字列として「INT」を入れて検索するとINT関数のヘルプが読める。以下にヘルプを引用してみる。
INT
指定した数値を超えない最大の整数を返します。
書式
INT(数値)
数値 切り捨てて整数にする実数を指定します。
まず、最初に関数名が入っていて、次に概要が書いてある。「指定した数値を超えない最大の整数」ということは、正の数に対しては小数点以下を取り除いた数値が戻り値になるが、負の値についてはちょっと異なる。たとえば -0.3を超えない最大の整数は 0ではなく -1であるから、INT(-0.3)は0ではなく -1 となる。このへんは「切り捨て」という言葉のイメージにだまされてしまうとはまる可能性がある。
練習問題2. オートSUMツールを使っていままで数式に入れてきた SUM関数についてヘルプで調べてみなさい
例題3. 「やりたいこと」から適切な関数を探す
Excelには300個以上の関数があるため、関数名からヘルプを調べるというのはあまり現実的ではない。実際にはなにかやりたい処理がまずあり、そのために必要な関数を探す場合の方が多い。ここでは、実数の小数点以下を切り捨てて整数化する方法をみる。
関数を探すためには、「関数の挿入」ツールを使うと便利。
Step 1. 関数の挿入ツールを起動する
関数を使った計算式を入れたいセルをアクティブセルにして、![]() をクリックする。
をクリックする。![]() は、数式バーの左側にある。
は、数式バーの左側にある。
![]()
Step 2. 関数の検索条件を入力する
関数の挿入ツールを起動すると、以下のような画面が開く。「関数の検索」という部分にやりたいことを書いて![]() をクリックすると、検索できる。
をクリックすると、検索できる。
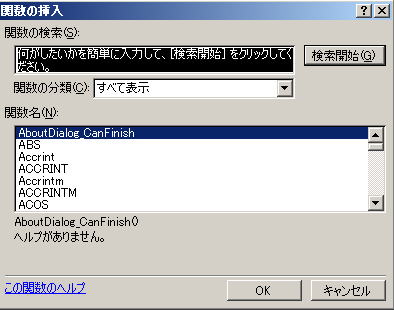
ここでは「切り捨て」と入力して![]() を押してみる。
を押してみる。
Step 3. 検索結果から適切な関数を選ぶ
「切り捨て」と関係がある関数がいくつか表示されるので、下に表示される簡単なヘルプを参考に適切なものを選ぶ。もし、より細かい情報が知りたければ、左下にある![]() をクリックすれば、関数の細かいヘルプが表示される。
をクリックすれば、関数の細かいヘルプが表示される。
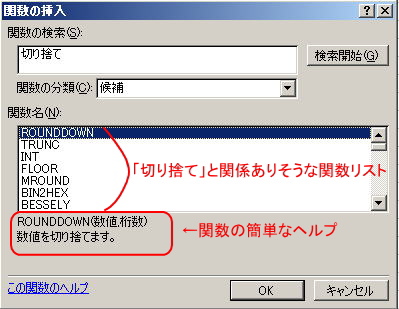
Step 4. 関数ヘルプを使って、ROUNDDOWN関数、TRUNC関数、FLOOR関数のヘルプを見ておく
Step 5. INT関数、ROUNDDOWN関数、FLOOR関数、TRUNC関数を実際に使って、以下の表を完成させてみる
関数を計算式の中に入力する際には、下の図のように直接関数名を手で入力してもよいし、Step3で適切な関数を選んだらOKを押して、関数に与える値を指定もよい。
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | ROUNDDOWN関数 | TRUNC関数 | FLOOR関数 | INT関数 | |
| 2 | -4.1 | =ROUNDDOWN(A2,0) | =TRUNC(A2) | =FLOOR(A2,1) | =INT(A2) |
| 3 | -0.5 | ? | ? | ? | ? |
| 4 | 0 | ? | ? | ? | ? |
| 5 | 0.5 | ? | ? | ? | ? |
| 6 | 4.1 | ? | ? | ? | ? |
練習問題3. 以下の作業をできそうな関数を、ヘルプを使って探してみなさい。また、指示された計算を探した関数を使って行ってみなさい。
例題4. 日経平均の終値を、移動平均を使って平滑化してみる
Step1. 日経平均株価(2007/1/4〜2007/9/28)のデータが入ったブック(stock_average.xls)をダウンロードする
Step2. 終値を折れ線グラフにしてみる
できあがりはこんな感じ。
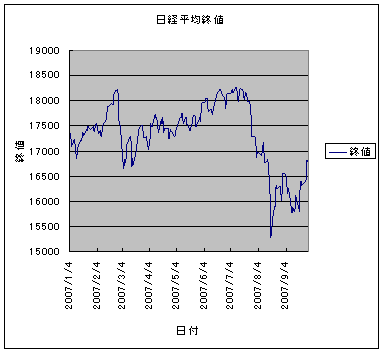
Step3. 数値軸の目盛範囲を変更する
終値の変化している範囲が15000〜18000円くらいの範囲なのに縦軸が0円からの目盛になっているので変化が分かりづらい。最小値を15000、最大値を19000に変更してみる。
目盛の最小値、最大値を変えるには? → Excel編 Q40 Column
できあがりはこんな感じ。
Step4. 1月4日〜1月11日の5日間移動平均を計算してみる
縦に変化を大きく出したら、今度は凸凹が沢山あって全体の見通しが悪くなった。このような時には、着目している日の前後何日かの範囲で平均をとっていく「移動平均」という方法を使うと近い範囲での凸凹が均されてわかりやすくなる。
株では、5日移動平均(着目している日の前々日、前日、当日、翌日、翌々日の平均)や25日移動平均(前12日+当日+後12日)などが短期の移動平均としてはよく使われる。当然のことながら、移動平均を取る場合はデータ期間の最初と最後は値が計算できない部分がでるため、あまり数が少ないデータでは使いづらい手法。
1. アクティブセルを、データ期間の最初から3日目の1月9日の移動平均欄(セルF4)に移動する
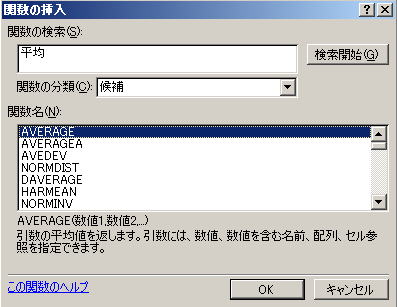
2. 関数の挿入ツールから平均を求める関数 AVERAGEを探す
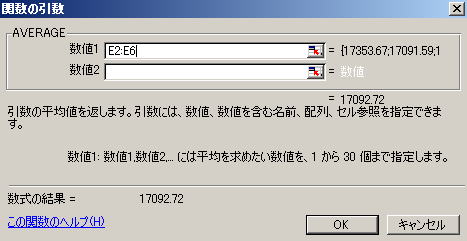
3. 数値1に、データを計算したい範囲E2:E6を指定する
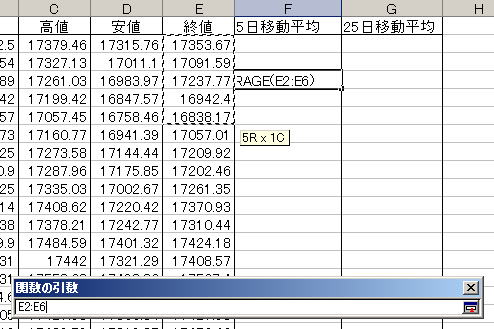
4, 範囲が正しく指定できたら、OKを押して関数をワークシートに入力する
Step 5. 計算式をコピーして、1月10日〜9月26日の間の日について5日間移動平均を計算する
※最後の2日(9/27, 9/28については、後の日のデータがないため移動平均が計算できない)
Step 6. 終値のグラフに5日移動平均のデータを追加する
Step 3で作成したグラフに、Step 5で計算した5日移動平均のデータを追加する
グラフにデータを追加するには? → Excel編 Q35
練習問題4. 例題4で作成したグラフに、25日移動平均のデータも追加しなさい
Tips: Excelで範囲を指定するには?
練習問題5.
score.xlsは仮想的な試験の得点を示したデータである。このデータを使って、5科目の合計得点、平均得点を計算し、さらに合計点でクラス内の順位をつけなさい。必要な関数は関数の挿入ツールを使って検索すること。
©2007, Hiroshi Santa OGAWA
このページにアダルトコンテンツ、XXXコンテンツ類は一切含まれていません。暴力反対.