第19課 散布図をExcelで描く

↑経済情報処理（2014）ホームページに戻る

準備問題
以下のデータを用いて、きつね食品、たぬき物産、いなり産業の売上高の積み重ね棒グラフを作成しなさい

冷凍うどん売上高（億円）	1月	2月	3月	4月	5月	6月	7月	8月	9月	10月	11月	12月
きつね食品	10	12	15	9	8	7	7	6	7	8	9	12
たぬき物産	8	8	8	8	8	8	8	8	8	8	8	8
いなり産業	10	12	14	16	18	20	22	24	26	28	30	32

1. 散布図をExcelで作ってみる

例題1. 簡単な散布図

以下の表は 身長、体重という 2つの変量の組み合わせを示している。この表を用いて、身長と体重の間の関係を考察しよう。

この表はたった10件のデータであるが、このデータをぱっと見せられて「身長と体重の関係は…」と説明するのは難しい。人間の脳みそは10件のデータを同時に扱えるところまでまだ進化していないので、それは致し方ないことである。そこで出てくるのが散布図。

Step 1. データを入力する

入力が面倒な人は、data09.xlsx の BMI シートを参照。

Step 2. データ範囲を選択する

下図のように、変数名（身長、体重）を含めてデータ範囲を選択する

Step 3. [挿入]タブから[グラフ]グループの[散布図]ボタンをクリックする

Step 4. グラフの種類を選ぶ

各データの間を線で結ぶ根拠がないので、線なしの散布図を選ぶ

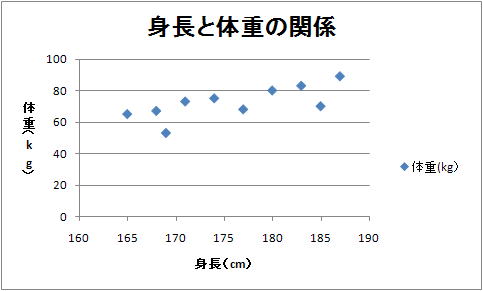
Step 5. あとは他のグラフと同じ。タイトル類は

グラフタイトル（T）

「身長と体重の関係」

X/数値軸(A)

身長（cm）

Y/数値軸(V)

体重（kg）

と入力しておこう。できあがりのグラフは下のような感じになる。グラフ上のそれぞれの点は、A〜Jの各サンプルでの身長と体重の組み合わせを表している。

Step 6. グラフの評価

作成したグラフをじっと眺めると、身長と体重の組み合わせを表す点は全体に右上がりに散らばっているように見える。データの散らばっている範囲を赤い線で囲ってみると下のような感じ。このような場合は身長と体重の間には正の相関がある可能性が高い。確かに常識的に考えても身長が高い人は低い人よりも体重が重めなのは当然な気がするので、おそらくそんな関係があるのだろう。

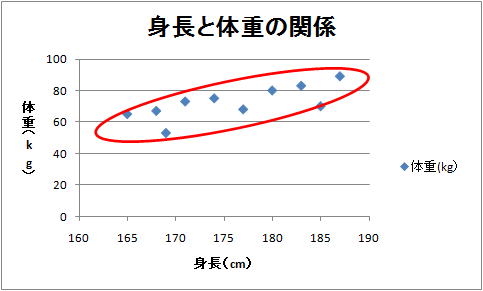
このように、データをグラフ化することで、単に数値の表をみてもよく分からなかった2変量の関係を人間が得意なパターン認識に持ち込むことができ、ぱっと見ただけで関係が読み取れるようになる。

↑経済情報処理（2014）ホームページに戻る

©2014, Hiroshi Santa OGAWA, Mai Okuda
このページにアダルトコンテンツ、XXXコンテンツ類は一切含まれていません。暴力反対.